Tiled Cholesky Factorization
We illustrate here the use of DataFlowTasks to parallelize a tiled Cholesky factorization. The implementation shown here is delibarately made as simple and self-contained as possible; yet, as we shall see when comparing to OpenBLAS, it is already quite performant!
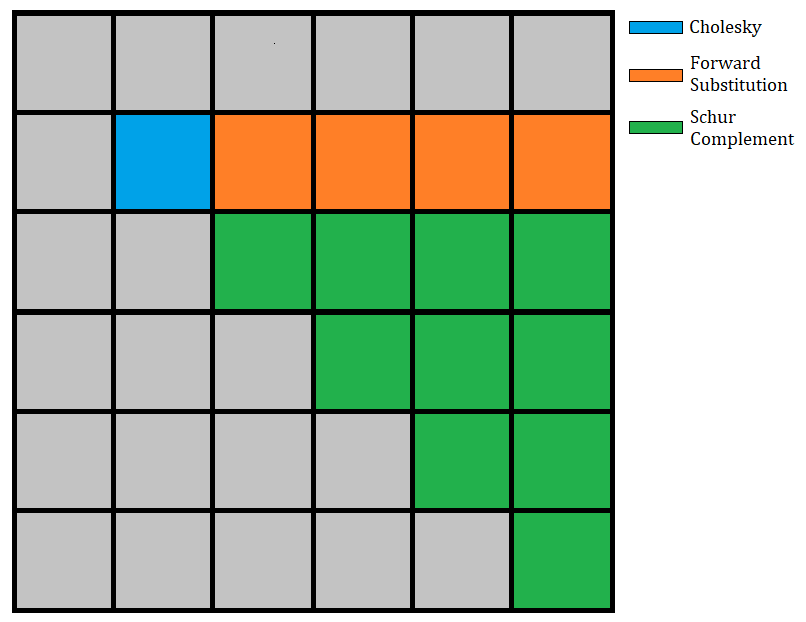
The Cholesky factorization algorithm takes a symmetric positive definite matrix $A$ and finds a lower triangular matrix $L$ such that $A = LLᵀ$. The tiled version of this algorithm decomposes the matrix $A$ into tiles (of even sizes, in this simplified version). At each step of the algorithm, we do a Cholesky factorization on the diagonal tile, use a triangular solve to update all of the tiles at the right of the diagonal tile, and finally update all the tiles of the submatrix with a schur complement.
If we have a matrix $A$ decomposed in $n \times n$ tiles, then the algorithm will have $n$ steps. The $i$-th step (with $i \in [1:n]$) performs:
- $1$ cholesky factorization of the $(i,i)$ tile,
- $(i-1)$ triangular solves (one for each tile in the $i$-th row of the upper triangular matrix),
- $i(i-1)/2$ matrix multiplications to update the submatrix.
These are the basic operations on tiles, which we are going to spawn in separate tasks in the parallel implementation. Accounting for all iterations, this makes a total of $\mathcal{O}(n^3)$ such tasks, decomposed as:
- $\mathcal{O}(n)$ cholesky factorizations,
- $\mathcal{O}(n^2)$ triangular solves,
- $\mathcal{O}(n^3)$ matrix multiplications.
The following image illustrates the 2nd step of the algorithm:
Sequential implementation
A sequential tiled factorization algorithm can be implemented as:
using LinearAlgebra
tilerange(ti, ts) = (ti-1)*ts+1:ti*ts
function cholesky_tiled!(A, ts)
m = size(A, 1); @assert m==size(A, 2)
m%ts != 0 && error("Tilesize doesn't fit the matrix")
n = m÷ts # number of tiles in each dimension
T = [view(A, tilerange(i, ts), tilerange(j, ts)) for i in 1:n, j in 1:n]
for i in 1:n
# Diagonal cholesky serial factorization
cholesky!(T[i,i])
# Left tiles update
U = UpperTriangular(T[i,i])
for j in i+1:n
ldiv!(U', T[i,j])
end
# Submatrix update
for j in i+1:n
for k in j:n
mul!(T[j,k], T[i,j]', T[i,k], -1, 1)
end
end
end
# Construct the factorized object
return Cholesky(A, 'U', zero(LinearAlgebra.BlasInt))
endcholesky_tiled! (generic function with 1 method)Let us build a small test case to check the correctness of the factorization. Here we divide a matrix of size 4096×4096 in 8×8 tiles of size 512×512:
n = 4096
ts = 512
A = rand(n, n)
A = (A + adjoint(A))/2
A = A + n*I;and the results seem to be correct:
F = cholesky_tiled!(copy(A), ts)
# Check results
err = norm(F.L*F.U-A,Inf)/max(norm(A),norm(F.L*F.U))
@show err
@assert err < eps(Float64)err = 1.7344504839115092e-17Parallel implementation
In order to parallelize the code with DataFlowTasks.jl, function calls acting on tiles are wrapped within @dspawn, along with annotations describing data access modes. We also give meaningful labels to the tasks, which will help debug and profile the code.
using DataFlowTasks
function cholesky_dft!(A, ts)
m = size(A, 1); @assert m==size(A, 2)
m%ts != 0 && error("Tilesize doesn't fit the matrix")
n = m÷ts # number of tiles in each dimension
T = [view(A, tilerange(i, ts), tilerange(j, ts)) for i in 1:n, j in 1:n]
for i in 1:n
# Diagonal cholesky serial factorization
@dspawn cholesky!(@RW(T[i,i])) label="chol ($i,$i)"
# Left tiles update
U = UpperTriangular(T[i,i])
for j in i+1:n
@dspawn ldiv!(@R(U)', @RW(T[i,j])) label="ldiv ($i,$j)"
end
# Submatrix update
for j in i+1:n
for k in j:n
@dspawn schur_complement!(@RW(T[j,k]), @R(T[i,j])', @R(T[i,k])) label="schur ($j,$k)"
end
end
end
# Construct the factorized object
r = @dspawn Cholesky(@R(A), 'U', zero(LinearAlgebra.BlasInt)) label="result"
return fetch(r)
end
schur_complement!(C, A, B) = mul!(C, A, B, -1, 1)schur_complement! (generic function with 1 method)Again, let us check the correctness of the result:
F = cholesky_dft!(copy(A), ts)
# Check results
err = norm(F.L*F.U-A,Inf)/max(norm(A),norm(F.L*F.U))
@show err
@assert err < eps(Float64)err = 1.7344504839115092e-17Debugging and Profiling
Let us now check what happens during a parallel run of our cholesky factorization. Thanks to the test above, the code is now compiled. Let's re-run it and collect meaningful profiling information:
# Clean profiling environment
GC.gc()
# Real workload to be analysed
Ac = copy(A)
log_info = DataFlowTasks.@log cholesky_dft!(Ac, ts)LogInfo with 121 logged tasks
The number of tasks being $\mathcal{O}(n^3)$, we can see how quickly the DAG complexity increases (even though the test case only has 8×8 tiles here):
DataFlowTasks.stack_weakdeps_env!()
using GraphViz
dag = GraphViz.Graph(log_info)The critical path, highlighted in red, includes all cholesky factorizations of diagonal tiles, as well as the required tasks in between them.
We can also readily get more details about the performance limiting factors:
DataFlowTasks.describe(log_info; categories=["chol", "ldiv", "schur"])• Elapsed time : 0.267
├─ Critical Path : 0.232
╰─ No-Wait : 0.185
• Run time : 2.136
├─ Computing : 1.481
│ ├─ chol : 0.054
│ ├─ ldiv : 0.395
│ ├─ schur : 1.031
│ ╰─ unlabeled : 0.000
├─ Task Insertion : 0.003
╰─ Other (idle) : 0.652and, at the price of loading Makie, display these in a more convenient profile plot:
using CairoMakie # or GLMakie in order to have more interactivity
trace = plot(log_info; categories=["chol", "ldiv", "schur"])
The overhead incurred by DataFlowTasks seems relatively small here: the time taken inserting tasks is barely measurable, and the scheduling did not lead to threads waiting idly for too long. This is confirmed by the bottom middle plot, showing a measured wall clock time not too much longer than the lower bound obtained when suppressing idle time.
The "Computing time: breakdown by category" plot seems to indicate that the matrix multiplications performed in the "Schur" tasks account for the majority of the computing time. This routine is probably already quite fast since it simply calls our BLAS library for a matrix-matrix product; it would be interesting, however, to see how LoopVectorization.jl fares here!
Performances
To benchmark the performance, we will compare our implementation to the one provided by our system's BLAS library. We will use OpenBlas here because it is the default BLAS library shipped with Julia, but if you have access to Intel's MKL, you should probably give it a try! Here is the benchmark:
using BenchmarkTools
BenchmarkTools.DEFAULT_PARAMETERS.seconds = 1
# n × n symmetric positive definite matrix
function spd_matrix(n)
A = rand(n, n)
A = (A + adjoint(A))/2
return A + n*I
end
function bench_blas(n)
nt = Threads.nthreads()
BLAS.set_num_threads(nt)
return @belapsed cholesky!(A) setup=(A=spd_matrix($n)) evals=1
end
function bench_tiled(n;tilesize=256)
BLAS.set_num_threads(1)
return @belapsed cholesky_tiled!(A, $tilesize) setup=(A=spd_matrix($n)) evals=1
end
function bench_dft(n;tilesize=256)
BLAS.set_num_threads(1)
return @belapsed cholesky_dft!(A, $tilesize) setup=(A=spd_matrix($n)) evals=1
endbench_dft (generic function with 1 method)Let us compare the performances of the default BLAS library and ours for various matrix sizes, and plot the results:
BLAS.get_config()LinearAlgebra.BLAS.LBTConfig
Libraries:
└ [ILP64] libopenblas64_.sonsizes = 512 .* (1:1:8)
tblas = map(bench_blas, nsizes)
tdft = map(bench_dft, nsizes)
Gflops = map(n->(1/3*n^3 + 1/2*n^2)/10^9, nsizes)
fig = Figure()
ax = Axis(fig[1,1], xlabel="Matrix size", ylabel="Time (s)")
scatterlines!(ax, nsizes, tblas, label= "OpenBLAS", linewidth=2)
scatterlines!(ax, nsizes, tdft, label="DFT", linewidth=2)
axislegend(position=:lt)
ax = Axis(fig[1,2], xlabel="Matrix size", ylabel="GFlops/second")
scatterlines!(ax, nsizes, Gflops ./ tblas, label= "OpenBLAS", linewidth=2)
scatterlines!(ax, nsizes, Gflops ./ tdft, label="DFT", linewidth=2)
axislegend(position=:lt)
Label(fig[0,:], "Cholesky factorization on $(Threads.nthreads()) threads", fontsize=20)
fig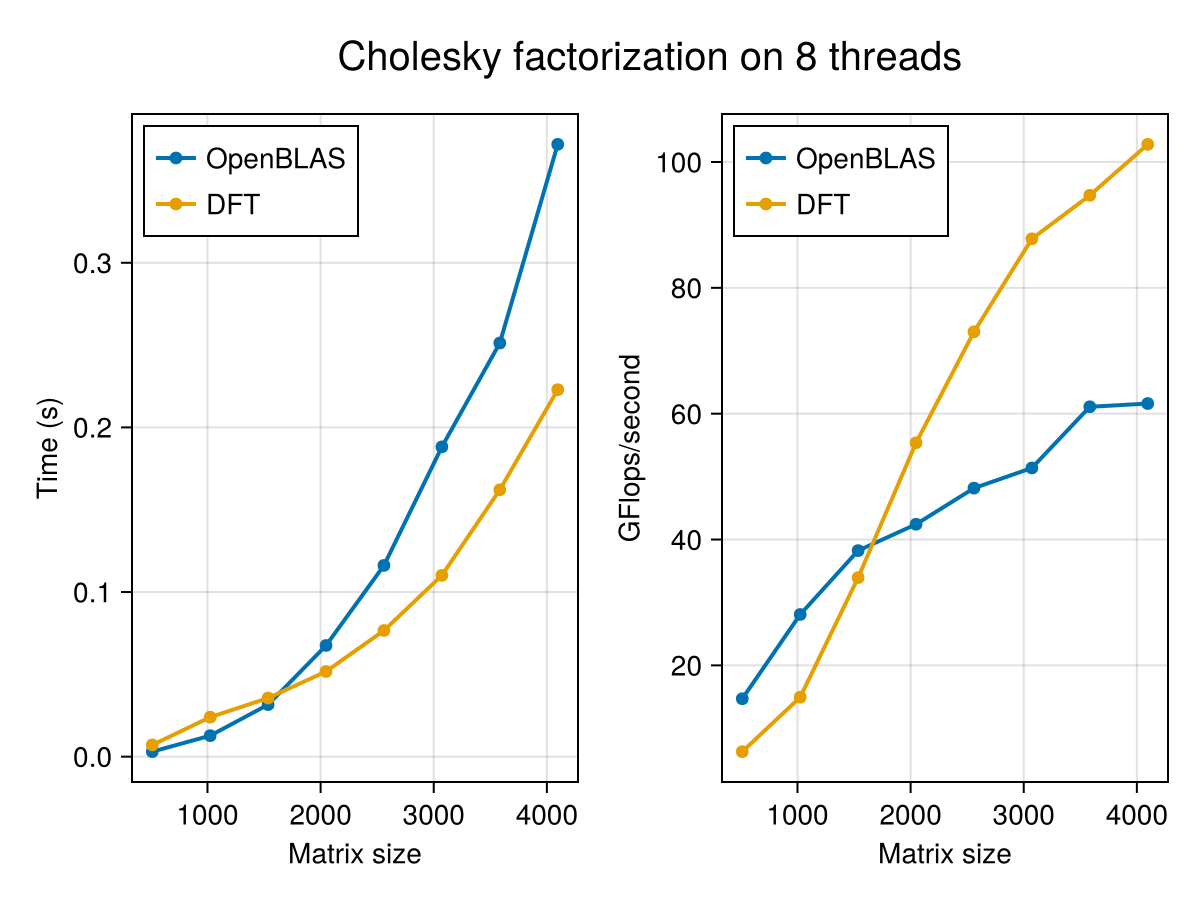
We see that, despite the simplicity of the implementation, the parallel version performs in par with the default BLAS library for the matrix sizes considered! For very large matrices, further optmizations are probably necessary to take into account the memory hierarchy of the machine. Finally, here is the observed speedup compared to a sequential tiled implementation and a matrix of size $n=4096$:
(;
threads = Threads.nthreads(),
speedup = bench_tiled(4096) / bench_dft(4096),
)(threads = 8, speedup = 5.449284705601107)This page was generated using Literate.jl.

